The dark arts of statistical genomics

-->

“Whereof one cannot speak, thereof one must be silent” - Wittgenstein

That’s a maxim to live by, or certainly to blog by, but I am about to break it. Most of the time I try to write about things I feel I have some understanding of (rightly or wrongly) or at least an informed opinion on. But I am writing this post from a position of ignorance and confusion.

I want to discuss a fairly esoteric and technical statistical method recently applied in human genetics, which has become quite influential. The results from recent studies using this approach have a direct bearing on an important question – the genetic architecture of complex diseases, such as schizophrenia and autism. And that, in turn, dramatically affects how we conceptualise these disorders. But this discussion will also touch on a much wider social issue in science, which is how highly specialised statistical claims are accepted (or not) by biologists or clinicians, the vast majority of whom are unable to evaluate the methodology.

Speak for yourself, you say! Well, that is exactly what I am doing.

The technique in question is known as Genome-wide Complex Trait Analysis (or GCTA). It is based on methods developed in animal breeding, which are designed to measure the “breeding quality” of an animal using genetic markers, without necessarily knowing which markers are really linked to the trait(s) in question. The method simply uses molecular markers across the genome to determine how closely an animal is related to some other animals with desirable traits. Its application has led to huge improvements in the speed and efficacy of selection for a wide range of traits, such as milk yield in dairy cows.   

GCTA has recently been applied in human genetics in an innovative way to explore the genetic architecture of various traits or common diseases. The term genetic architecture refers to the type and pattern of genetic variation that affects a trait or a disease across a population. For example, some diseases are caused by mutations in a single gene, like cystic fibrosis. Others are caused by mutations in any of a large number of different genes, like congenital deafness, intellectual disability, retinitis pigmentosa and many others. In these cases, each such mutation is typically very rare – the prevalence of the disease depends on how many genes can be mutated to cause it.

For common disorders, like heart disease, diabetes, autism and schizophrenia, this model of causality by rare, single mutations has been questioned, mainly because such mutations have been hard to find. An alternative model is that those disorders arise due to the inheritance of many risk variants that are actually common in the population, with the idea that it takes a large number of them to push an individual over a threshold of burden into a disease state. Under this model, we would all carry many such risk variants, but people with disease would carry more of them.

That idea can be tested in genome-wideassociation studies (GWAS). These use molecular methods to look at many, many sites in the genome where the DNA code is variable (it might be an “A” 30% of the time and a “T” 70% of the time). The vast majority of such sites (known as single-nucleotide polymorphisms or SNPs) are not expected to be involved in risk for the disease, but, if one of the two possible variants at that position is associated with an increased risk for the disease, then you would expect to see an increased frequency of that variant (say the “A” version) in a cohort of people affected by the disease (cases) versus the frequency in the general population (controls). So, if you look across the whole genome for sites where such frequencies differ between cases and controls you can pick out risk variants (in the example above, you might see that the “A” version is seen in 33% of cases versus 30% of controls). Since the effect of any one risk variant is very small by itself, you need very large samples to detect statistically significant signals of a real (but small) difference in frequency between cases and controls, amidst all the noise.  

GWAS have been quite successful in identifying many variants showing a statistical association with various diseases. Typically, each one has a tiny statistical effect on risk by itself, but the idea is that collectively they increase risk a lot. But how much is a lot? That is a key question in the field right now. Perhaps the aggregate effects of common risk variants explain all or the majority of variance in the population in who develops the disease. If that is the case then we should invest more efforts into finding more of them and figuring out the mechanisms underlying their effects.

Alternatively, maybe they play only a minor role in susceptibility to such conditions. For example, the genetic background of such variants might modify the risk of disease but only in persons who inherit a rare, and seriously deleterious mutation. This modifying mechanism might explain some of the variance in the population in who does and does not develop that disease, but it would suggest we should focus more attention on finding those rare mutations than on the modifying genetic background. 

For most disorders studied so far by GWAS, the amount of variance collectively explained by the currently identified common risk variants is quite small, typically on the order of a few percent of the total variance.

But that doesn’t really put a limit on how much of an effect all the putative risk variants could have, because we don’t know how many there are. If there is a huge number of sites where one of the versions increases risk very, very slightly (infinitesimally), then it would require really vast samples to find them all. Is it worth the effort and the expense to try and do that? Or should we be happy with the low-hanging fruit and invest more in finding rare mutations? 

This is where GCTA analyses come in. The idea here is to estimate the total contribution of common risk variants in the population to determining who develops a disease, without necessarily having to identify them all individually first. The basic premise of GCTA analyses is to not worry about picking up the signatures of individual SNPs, but instead to use all the SNPs analysed to simply measure relatedness among people in your study population. Then you can compare that index of (distant) relatedness to an index of phenotypic similarity. For a trait like height, that will be a correlation between two continuous measures. For diseases, however, the phenotypic measure is categorical – you either have been diagnosed with it or you haven’t.

So, for diseases, what you do is take a large cohort of affected cases and a large cohort of unaffected controls and analyse the degree of (distant) genetic relatedness among and between each set. What you are looking for is a signal of greater relatedness among cases than between cases and controls – this is an indication that liability to the disease is: (i) genetic, and (ii) affected by variants that are shared across (very) distant relatives.

The logic here is an inversion of the normal process for estimating heritability, where you take people with a certain degree of genetic relatedness (say monozygotic or dizygotic twins, siblings, parents, etc.) and analyse how phenotypically similar they are (what proportion of them have the disease, given a certain degree of relatedness to someone with the disease). For common disorders like autism and schizophrenia, the proportion of monozygotic twins who have the disease if their co-twin does is much higher than for dizygotic twins. The difference between these rates can be used to estimate how much genetic differences contribute to the disease (the heritability).

With GCTA, you do the opposite – you take people with a certain degree of phenotypic similarity (they either are or are not diagnosed with a disease) and then analyse how genetically similar they are.

If a disorder were completely caused by rare, recent mutations, which would be highly unlikely to be shared between distant relatives, then cases with the disease should not be any more closely related to each other than controls are. The most dramatic examples of that would be cases where the disease is caused by de novo mutations, which are not even shared with close relatives (as in Down syndrome). If, on the other hand, the disease is caused by the effects of many common, ancient variants that float through the population, then enrichment for such variants should be heritable, possibly even across distant degrees of relatedness. In that situation, cases will have a more similar SNP profile than controls do, on average.

Now, say you do see some such signal of increased average genetic relatedness among cases. What can you do with that finding? This is where the tricky mathematics comes in and where the method becomes opaque to me. The idea is that the precise quantitative value of the increase in average relatedness among cases compared to that among controls can be extrapolated to tell you how much of the heritability of the disorder is attributable to common variants. How this is achieved with such specificity eludes me.

Let’s consider how this has been done for schizophrenia. A 2012 study by Lee and colleagues analysed multiple cohorts of cases with schizophrenia and controls, from various countries. These had all been genotyped for over 900,000 SNPs in a previous GWAS, which hadn’t been able to identify many individually associated SNPs.

Each person’s SNP profile was compared to each other person’s profile (within and between cohorts), generating a huge matrix. The mean genetic similarity was then computed among all pairs of cases and among all pairs of controls. Though these are the actual main results – the raw findings – of the paper, they are remarkably not presented in the paper. Instead, the results section reads, rather curtly:

Using a linear mixed model (see Online Methods), we estimated the proportion of variance in liability to schizophrenia explained by SNPs (h2) in each of these three independent data subsets. … The individual estimates of h2 for the ISC and MGS subsets and for other samples from the PGC-SCZ were each greater than the estimate from the total com­bined PGC-SCZ sample of h2 = 23% (s.e. = 1%)

So, some data we are not shown (the crucial data) are fed into a model and out pops a number and a strongly worded conclusion: 23% of the variance in the trait is tagged by common SNPs, mostly functionally attributable to common variants*. *[See important clarification in the comments below - it is really the entire genetic matrix that is fed into the models, not just the mean relatedness as I suggested here. Conceptually, the effect is still driven by the degree of increased genetic similarity amongst cases, however]. This number has already become widely cited in the field and used as justification for continued investment in GWAS to find more and more of these supposed common variants of ever-decreasing effect.

Now I’m not saying that that number is not accurate but I think we are right to ask whether it should simply be taken as an established fact. This is especially so given the history of how similar claims have been uncritically accepted in this field. 

In the early 1990s, a couple of papers came out that supposedly proved, or at least were read as proving, that schizophrenia could not be caused by single mutations. Everyone knew it was obviously not always caused by mutations in one specific gene, in the way that cystic fibrosis is. But these papers went further and rejected the model of genetic heterogeneity that is characteristic of things like inherited deafness and retinitis pigmentosa. This was based on a combination of arguments and statistical modelling.

The arguments were that if schizophrenia were caused by single mutations, they should have been found by the extensive linkage analyses that had already been carried out in the field. If there were a handful of such genes, then this criticism would have been valid, but if that number were very large then one would not expect consistent linkage patterns across different families. Indeed, the way these studies were carried out – by combining multiple families – would virtually ensure you would not find anything. The idea that the disease could be caused by mutations in any one of a very large number (perhaps hundreds) of different genes was, however, rejected out of hand as inherently implausible. [See here for a discussion of why a phenotype like that characterising schizophrenia might actually be a common outcome].

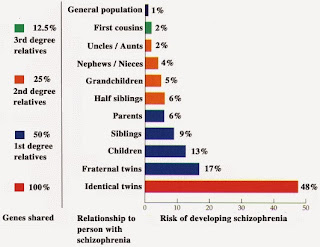
The statistical modelling was based on a set of numbers – the relative risk of disease to various family members of people with schizophrenia. Classic studies found that monozygotic twins of schizophrenia cases had a 48% chance (frequency) of having that diagnosis themselves. For dizygotic twins, the frequency was 17%. Siblings came in about 10%, half-sibs about 6%, first cousins about 2%. These figures compare with the population frequency of ~1%.

The statistical modelling inferred that this pattern of risk, which decreases at a faster than linear pace with respect to the degree of genetic relatedness, was inconsistent with the condition arising due to single mutations. By contrast, these data were shown to be consistent with an oligogenic or polygenic architecture in affected individuals.

There was however, a crucial (and rather weird) assumption – that singly causal mutations would all have a dominant mode of inheritance. Under that model, risk would decrease linearly with distance of relatedness, as it would be just one copy of the mutation being inherited. This contrasts with recessive modes requiring inheritance of two copies of the mutation, where risk to distant relatives drops dramatically. There was also an important assumption of negligible contribution from de novo mutations. As it happens, it is trivial to come up with some division of cases into dominant, recessive and de novo modes of inheritance that collectively generate a pattern of relative risks similar to observed. (Examples of all such modes of inheritance have now been identified). Indeed, there is an infinite number of ways to set the (many) relevant parameters in order to generate the observed distribution of relative risks. It is impossible to infer backwards what the actual parameters are. Not merely difficult or tricky or complex – impossible.

Despite these limitations, these papers became hugely influential. The conclusion – that schizophrenia could not be caused by mutations in (many different) single genes – became taken as a proven fact in the field. The corollary – that it must be caused instead by combinations of common variants – was similarly embraced as having been conclusively demonstrated.

This highlights an interesting but also troubling cultural aspect of science – that some claims are based on methodology that many of the people in the field cannot evaluate. This is especially true for highly mathematical methods, which most biologists and psychiatrists are ill equipped to judge. If the authors of such claims are generally respected then many people will be happy to take them at their word. In this case, these papers were highly cited, spreading the message beyond those who actually read the papers in any detail.

In retrospect, these conclusions are fatally undermined not by the mathematics of the models themselves but by the simplistic assumptions on which they are based. With that precedent in mind, let’s return to the GCTA analyses and the strong claims derived from them.

Before considering how the statistical modelling works (I don’t know) and the assumptions underlying it (we’ll discuss these), it’s worth asking what the raw findings actually look like.

While the numbers are not provided in this paper (not even in the extensive supplemental information), we can look at similar data from a study by the same authors, using cohorts for several other diseases (Crohn’s disease, bipolar disorder and type 1 diabetes).

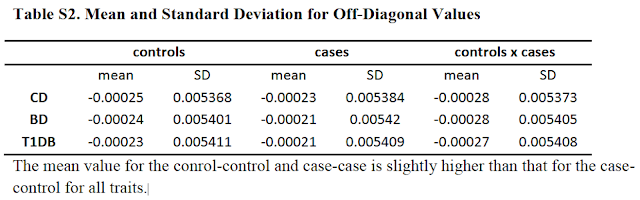
Those numbers are a measure of mean genetic similarity (i) among cases, (ii) among controls and (iii) between cases and controls. The important finding is that the mean similarity among cases or among controls is (very, very slightly) greater than between cases and controls. All the conclusions rest on this primary finding. Because the sample sizes are fairly large and especially because all pairwise comparisons are used to derive these figures, this result is highly statistically significant. But what does it mean?

The authors remove any persons who are third cousins or closer, so we are dealing with very distant degrees of genetic relatedness in our matrix. One problem with looking just at the mean level of similarity between all pairs is it tells us nothing about the pattern of relatedness in that sample.

Is the small increase in mean relatedness driven by an increase in relatedness of just some of the pairs (equivalent to an excess of fourth or fifth cousins) or is it spread across all of them? Is there any evidence of clustering of multiple individuals into subpopulations or clans? Does the similarity represent “identity by descent” or “identity by state”? The former derives from real genealogical relatedness while the latter could signal genetic similarity due to chance inheritance of a similar profile of common variants – presumably enriched in cases by those variants causing disease. (That is of course what GWAS look for).  

If the genetic similarity represents real, but distant relatedness, then how is this genetic similarity distributed across the genome, between any two pairs? The expectation is that it would be present mainly in just one or two genomic segments that happen to have been passed down to both people from their distant common ancestor. However, that is likely to track a slight increase in identity by state as well, due to subtle population/deep pedigree structure. Graham Coop put it this way in an email to me: “Pairs of individuals with subtly higher IBS genome-wide are slightly more related to each other, and so slightly more likely to share long blocks of IBD.”

If we are really dealing with members of a huge extended pedigree (with many sub-pedigrees within it) – which is essentially what the human population is – then increased phenotypic similarity could in theory be due to either common or rare variants shared between distant relatives. (They would be different rare variants in different pairs). 

So, overall, it’s very unclear (to me at least) what is driving this tiny increase in mean genetic similarity among cases. It certainly seems like there is a lot more information in those matrices of relatedness (or in the data used to generate them) than is actually used – information that may be very relevant to interpreting what this effect means.

Nevertheless, this figure of slightly increased mean genetic similarity can be fed into models to extrapolate the heritability explained – i.e., how much of the genetic effects on predisposition to this disease can be tracked by that distant relatedness. I don’t know how this model works, mathematically speaking. But there are a number of assumptions that go into it that are interesting to consider.

First, the most obvious explanation for an increased mean genetic similarity among cases is that they are drawn from a slightly different sub-population than controls. This kind of cryptic population stratification is impossible to exclude in ascertainment methods and instead must be mathematically “corrected for”. So, we can ask, is this correction being applied appropriately? Maybe, maybe not – there certainly is not universal agreement among the Illuminati on how this kind of correction should be implemented or how successfully it can account for cryptic stratification.

The usual approach is to apply principal components analysis to look for global trends that differentiate the genetic profiles of cases and controls and to exclude those effects from the models interpreting real heritability effects. Lee and colleagues go to great lengths to assure us that these effects have been controlled for properly, excluding up to 20 components. Not everyone agrees that these approaches are sufficient, however.

Another major complication is that the relative number of cases and controls analysed does not reflect the prevalence of the disease in the population. In these studies, there were about equal numbers of each in fact, versus a 1:100 ratio of cases to controls in the general population for disorders like schizophrenia or autism. Does this skewed sampling affect the results? One can certainly see how it might. If you are looking to measure an effect where, say, the fifth cousin of someone with schizophrenia is very, very slightly more likely to have schizophrenia than an unrelated person, then ideally you should sample all the people in the population who are fifth cousins and see how many of them have schizophrenia. (This effect is expected to be almost negligible, in fact. We already know that even first cousins have only a modestly increased risk of 2%, from a population baseline of 1%. So going to fifth cousins, the expected effect size would likely only be around 1.0-something, if it exists at all).

You’d need to sample an awful lot of people at that degree of relatedness to detect such an effect, if indeed it exists at all. GCTA analyses work in the opposite direction, but are still trying to detect that tiny effect. But if you start with a huge excess of people with schizophrenia in your sample, then you may be missing all the people with similar degrees of relatedness who did not develop the disease. This could certainly bias your impression of the effect of genetic relatedness across this distance.

Lee and colleagues raise this issue and spend a good deal of time developing new methods to statistically take it into account and correct for it. Again, I cannot evaluate whether their methods really accomplish that goal. Generally speaking, if you have to go to great lengths to develop a novel statistical correction for some inherent bias in your data, then some reservations seem warranted.

So, it seems quite possible, in the first instance, that the signal detected in these analyses is an artefact of cryptic population substructure or ascertainment. But even if it we take it as real, it is far from straightforward to divine what it means.

The model used to extrapolate heritability explained has a number of other assumptions. First, is that all genetic interactions are additive in nature. [See here for arguments why that is unlikely to reflect biological reality]. Second, it assumes that the relationship between genetic relatedness and phenotypic similarity is linear and can be extrapolated across the entire range of relatedness. At least, all you are supposedly measuring is the tiny effect at extremely low genetic relatedness – can this really be extrapolated to effects at close relatedness? We’ve already seen that this relationship is not linear as you go from twins to siblings to first cousins – those were the data used to argue for a polygenic architecture in the first place.

This brings us to the final assumption implicit in the mathematical modelling – that the observed highly discontinuous distribution of risk to schizophrenia actually reflects a quantitative trait that is continuously (and normally) distributed across the whole population. A little sleight of hand can convert this continuous distribution of “liability” into a discontinuous distribution of cases and controls, by invoking a threshold, above which disease arises. While genetic effects are modelled as exclusively linear on the liability scale, the supposed threshold actually represents a sudden explosion of epistasis. With 1,000 risk variants you’re okay, but with say 1,010 or 1,020 you develop disease. That’s non-linearity for free and I’m not buying it.

I also don’t buy an even more fundamental assumption – that the diagnostic category we call “schizophrenia” is a unitary condition that defines a singular and valid biological phenotype with a common etiology. Of course we know it isn’t – it is a diagnosis of exclusion. It simply groups patients together based on a similar profile of superficial symptoms, but does not actually imply they all suffer from the same condition. It is a place-holder, a catch-all category of convenience until more information lets us segregate patients by causes. So, the very definition of cases as a singular phenotypic category is highly questionable.

Okay, that felt good.

But still, having gotten those concerns off my chest, I am not saying that the conclusions drawn from the GCTA analyses of disorders like schizophrenia and autism are not valid. As I’ve said repeatedly here, I am not qualified to evaluate the statistical methodology. I do question the assumptions that go into them, but perhaps all those reservations can be addressed. More broadly, I question the easy acceptance in the field of these results as facts, as opposed to the provisional outcome of arcane statistical exercises, the validity of which remains to be established. 

“Facts are stubborn things, but statistics are pliable.” – Mark Twain